Deret Geometri

Saat ini banyak sistem penjualan yang menggunakan sistem Multi Level Marketing (MLM). Dalam sistem ini seseorang mengembangkan bisnisnya misalnya dengan mencari 2 agen di bawahnya yang memasarkan produk. Kemudian masing-masing agen tersebut mencari dua agen lagi di bawahnya dan seterusnya. Keuntungan yang diperoleh orang pertama sangat bergantung pada hasil kerja yang diperoleh para agen di bawahnya.
Perhatikan bahwa banyaknya orang yang terlibat dalam bisnis itu adalah 1 + 2 + 4 + 8 + …
Banyaknya orang yang terlibat dalam bisnis itu merupakan contoh dari deret geometri.

Deret geometri merupakan penjumlahan dari suku-suku barisan geometri. Jumlah $n$ suku pertama pada deret geometri ($S_n$) dirumuskan sebagai berikut.
$S_n=\frac{a(1-r^n)}{1-r}$, untuk $r < 1$
atau
$S_n=\frac{a(r^{n-1})}{r-1}$, untuk $r > 1$

Keterangan:
$n=$ banyak suku
$a=$ suku pertama
$r=$ rasio

Contoh:
Sebatang pipa dipotong menjadi 5 bagian. Potongan pipa pertama berukuran 5 cm dan potongan kedua berukuran 15 cm. Berapakah panjang pipa semula?

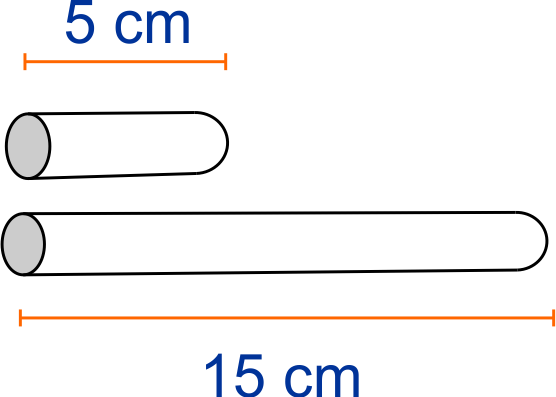
Gambar 1. Potongan Pipa
Penyelesaian:
Dik: $a=5; n=5$
Dit: Panjang pipa semula$=S_5$?
$r=\frac{15}{5}=3, r > 1$
$S_n=\frac{a(r^n-1)}{r-1}$
$S_5=\frac{5×(3^7-1)}{3-1}$
     $=\frac{5×(243-1)}{2}$
     $= \frac{5×242}{2}$
     $= \frac{1.210}{2}$
     $=605$
Jadi, panjang pipa semula adalah 605 cm.

Deret Geometri Tak Hingga

Deret geometri tak hingga adalah deret geometri yang memiliki suku tak terhingga. Terdapat dua jenis deret geometri tak hingga, yaitu sebagai berikut.

1. Deret geometri konvergen
Jika deret geometri bersifat konvergen atau memiliki limit jumlah, maka $$S_∞=\frac{a}{1-r}, dengan -1 < r < 1$$ Keterangan:
$S_∞$= jumlah deret geometri tak hingga
Dari rumus tersebut diperoleh:
$a=(1-r) S_∞$ untuk menentukan suku pertama deret geometri tak hingga.
$r=1-\frac{a}{s_∞}$ untuk menentukan rasio deret geometri tak hingga.
Agar lebih memahami jumlah dari deret geometri tak hingga yang konvergen, perhatikan ilustrasi berikut.
Misalkan selembar kertas berbentuk persegi panjang dibagi menjadi dua dan salah satu bagiannya dibagi lagi menjadi dua bagian dan begitu seterusnya.

Gambar 2. Potongan Kertas

Contoh lain adalah sebagai berikut:
Perhatikan video animasi di atas. Sebuah bola dijatuhkan ke lantai dari ketinggian 8 meter. Setiap kali menyentuh lantai, bola tersebut memantul dengan tinggi pantulan bola $\frac{3}{4}$ kali dari tinggi sebelumnya. Tentukan panjang lintasan sampai bola tersebut berhenti.
Penyelesaian:
Berdasarkan simulasi tersebut, diperoleh $U_1=8, U_2=8(\frac{3}{4})=6, U_3=6(\frac{3}{4})=\frac{9}{2}$, dan seterusnya. Panjang lintasan bola terdiri atas dua deret geometri konvergen.
Lintasan bola ke bawah atau jatuh
$8+6+\frac{9}{2}+...$
$a=8$
$r=\frac{6}{8}= \frac{3}{4}=0,75$
$S_{∞1}=\frac{a}{1-r}$
        $=\frac{8}{1-0,75}$
        $=\frac{8}{0,25}$
        $=32$
Lintasan saat bola ke atas atau memantul
Karena tinggi bola memantul $\frac{3}{4}$ kali dari tinggi sebelumnya, maka
$6+\frac{9}{2}+...$
$a=6$
$r=\frac{\frac{9}{2}}{6}$
   $=\frac{9}{2}×\frac{1}{6}$
   $=\frac{9}{12}= 0,75$
$S_{∞2}=\frac{a}{1-r}$
        $=\frac{6}{1-0,75}$
        $=\frac{6}{0,25}$
        $=24$
Jadi, jumlah lintasan bola seluruhnya adalah $S_{∞1}+S_{∞2}$
32 meter+24 meter = 56 meter.

2. Deret geometri divergen (memencar)
Jika $r\leq-1$ atau $r≥1$, maka deret geometri tak hingga akan divergen, yaitu jumlah suku-sukunya tidak terbatas atau tidak menuju suatu bilangan tertentu dan tidak memiliki limit jumlah.
Contoh:
Tentukan jumlah tak hingga dari deret $\frac{1}{4}+1+4+16+...$
Penyelesaian:
$r=\frac{1}{\frac{1}{4}}=4>1$, maka jumlah deret tak hingganya tidak ada.

Nah, kamu sudah menyelesaikan materi deret geometri. Selanjutnya kamu bisa mengerjakan soal latihan dengan menekan tombol di bawah.